13 有限单元理论
在本节中，将详细介绍OPTUM G2中可用的实体单元。 其中包括导致对精确解决方案进行严格上限和下限单元，以及通常更准确但不会导致对解决方案进行严格限制的“混合”单元。
13.1 下限单元
考虑弹塑性下限原理：
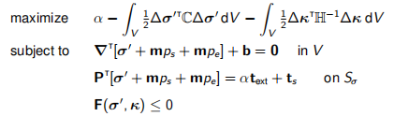(13.1).
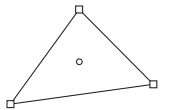
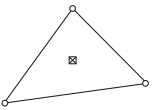
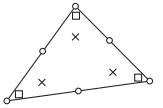
如第8节所示，满足此问题约束的任何应力场都会导致目标函数的下限估计，在刚塑性（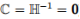
）的情况下目标函数为破坏乘数。考虑到涉及一阶导数的平衡方程，并考虑到必须在任何地方都满足屈服函数，下限单元的明显候选者是其角节点之间的应力线性变化的三角形单元。 图13.1所示的该元件能够满足上述所有限制，要求该单元上单位重量b恒定，每个单元内的渗流压力ps线性变化，且三个角节点满足屈服条件。
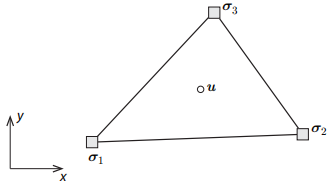
图 13.1: 下限单元
对于应力和超静孔隙压力，我们引入以下有限元近似值：
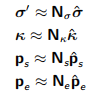(13.2)
Nσ，Nκ，Ns和Ne分别是节点有效应力、硬化变量、稳态孔隙压力和超静定压力分别包含线性函数。通常，以与应力相同的方式，即通过线性形状函数，内插硬化变量和超静定压力。
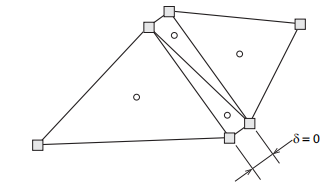
图13.2：下限单元与两个零厚度单元相连以产生静态允许的不连续性应力
离散平衡方程可以写成
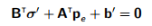（13.3）
其中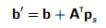
(13.4)
同时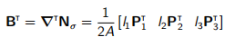
(13.5)
且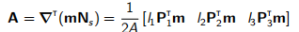
(13.6)
可以将上述平衡方程乘以单元面积A，以获得即使对于零厚度单元也有效的一组方程。此属性可用于构造单元之间的静态允许应力不连续点。典型案例显示在图（13.2） 中，其中两个“连接单元”通过完全相同类型的零厚度单元连接。在零厚度贴片中建立的四个平衡方程沿着整个界面在界面的每个端部有效地连续性施加了法向应力和剪应力。
用标准高斯求积法对（13.1）的目标函数中的二次项求解，使得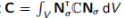
和
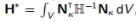，最终要求解的离散优化为：
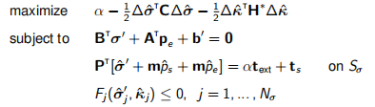(13.7)
其中在每个Nσ应力点都施加了屈服条件。
上面的公式是最初为极限分析应用构想的标准下限单元的概括（请参阅Bottero等人1980； Lyamin 1999； Lyamin和Sloan 2002a； Lysmer 1970； Sloan 1988及其参考）。
考虑弹塑性Hellinger-Reissner原理：
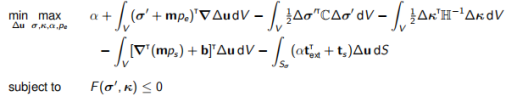(13.8)
通过为所涉及的变量指定近似值（即有效应力，孔隙压力和位移）来离散化该原理。 使用标准的有限单元术语，这些由
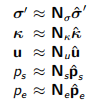(13.9)
尽管原则上可以自由选择各种形状函数，但我们将做出以下假设：i）在单元之间的位移是连续的； ii）应力，硬化变量和超静定压力以相同的方式近似，并且在单元之间是不连续的；iii）前者的多项式比后者高阶。 基于这些假设，标准的有限单元直接应用虚功原理的，并可以将特殊情况复制为仅涉及未知的位移。
将以上近似值插入到（13.8）中会导致以下离散问题：
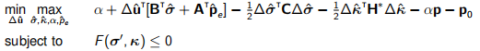(13.10)
其中
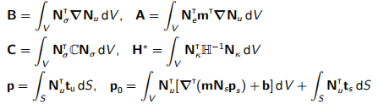(13.11)
可以针对增量位移解决问题（13.10），最终问题转化为：
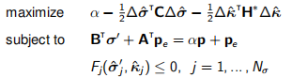(13.12)
上述公式类似于Krabbenhoft和Lyamin（2012）提出的公式，是Krabbenhoft等人早期公式的概括。 （2007a，b）。
13.2.1高斯和拉格朗日
如上所述，使用比位移的多项式低一阶多项式的形状函数对应力进行插值。此外，位移形状函数始终是拉格朗日多项式，其节点位于所谓的拉格朗日点上。另外，应力点的位置不太明显 可能性是高斯点，也可能性是拉格朗日点。在OPTUM G2中，考虑了每种可能性，并且相应的单元被相应地标记（高斯或拉格朗日）。
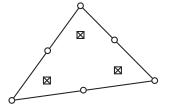
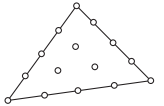
图13.3中显示了一个示例。此处的位移呈二次方变化，而应力线性变化。对于高斯单元，应力点是具有重心坐标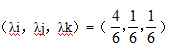
的高斯点，而拉格朗日单元使用角节点作为插值点。
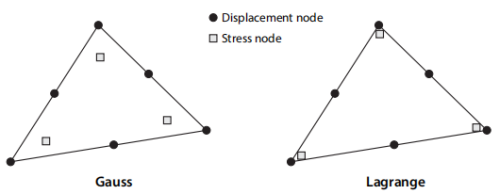
图13.3：高斯和拉格朗日类型的二阶位移/线性应力三角形。
13.2.2上限单元
上限单元可以直接基于上限原理，例如（6.17）构造。或者，它们可以作为混合单元的特殊情况派生。后一种方法在许多方面都是可取的，因为它避免了对耗散函数的任何显式使用（原则上可以在屈服函数可用时完成，但可能无法直接推导得出）。
两个上限单元是可能的：线性位移/恒定应力三角形（请参见Lyamin和Sloan 2002b； Sloan 1989，及其中的参考文献）和由Yu等人首先提出的二次位移/线性应力三角形。（1994）。前者只可能是混合单元。后者为混合单元的特例，其中应力是根据拉格朗日点进行插值的，而拉格朗日点被用作等式（13.11）中矩阵B和A的积分点。 Krabbenhoft等人讨论了上限单元作为混合单元的特殊情况的公式。（2007a，b）。
| 下限 应力的线性插值。单元之间包括静态允许的应力不连续性。 注意：此单元会在破坏负荷上产生严格的下限值。每个单元内的位移是恒定的。 |
| 上限 位移的二次插值和应力的线性插值。 使用三角形顶点对B矩阵进行积分。 注意：此单元在破坏负载上产生严格的上限。 单元之间的位移是连续的。 |
| 6节点高斯 位移的二次插值和应力的线性插值。 使用高斯点精确积分B矩阵 注意：尽管不严格，但此单元产生的破坏乘数趋于从上限收敛。 |
| 15节点高斯 位移的四次插值和应力的三次插值（未显示）。 B矩阵使用高斯正交精确积分。 注意：尽管不严格，但此单元产生的破坏乘数趋于从上限收敛。 |
| 3节点高斯（其他） 位移和恒定应力的线性插值。 运动学上允许的单元之间位移不连续。 注意：此单元在破坏负载上产生严格的上限。 对于高度受限的问题，可能会比上限产生更好的结果。 |
| 6节点拉格朗日（其他） 位移的二次插值和应力的线性插值。 B矩阵被精确地积分。 在以近似方式施加流动法则的同时，整个单元都满足屈服条件。 注意：与6节点高斯单元相比，此单元趋向于导致更准确的结果。 但是，不应将其用于纯摩擦材料 |
位移节点 
应力节点 
积分点
图13.4：OPTUM G2中可用单元选项
13.2.3单元概述
图13.4给出了OPTUM G2中某些可用单元的概述。
13.2.4不连续
不连续性可能是通过设置零厚度规则连续单元引入（有关详细信息，请参见Krabbenhoft等人2005； Lyamin等人2005. 2011）。 默认情况下，所有实体域之间都包括此类不连续性。
