案例57:随机分析 – 入门案例
本案例介绍了OptumG2中随机分析的可能性,特别是材料参数空间变异性的随机场建模概念。为此,考虑了条形基础位于Tresca材料模型中的情况,其中材料模型中的不排水抗剪强度是随机变化的(如图57.1所示)。基础上的荷载q = 249 kN/m2,对于su = 80 kPa,得到的FS = 5.14 su / q = 1.65。
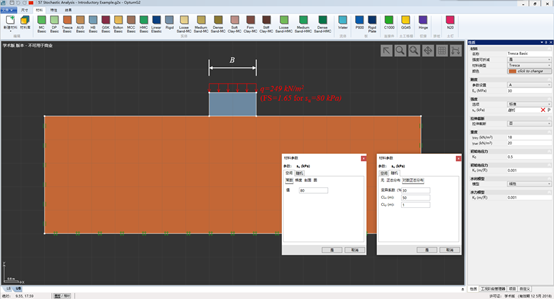
图57.1 条形基础位于随机不排水抗剪强度的黏土上
57.1 材料参数的变异性
天然土体呈现出相当大的变异性,其起源可以追溯到一系列长度尺度的各种方法。这种变异性可以在许多方面进行考虑。最简单的方法是,假设一个给定的参数,比如不排水抗剪强度,服从平均值和标准偏差的概率分布。这种参数的变异性通常可以用对数正态分布来模拟:
![]() (57.1)
(57.1)
其中,f 是参数 x,μ,σ 的概率分布函数,这些参数是与平均值和标准偏差有关的模型参数,平均值和标准偏差为:
![]() (57.2)
(57.2)
![]() (57.3)
(57.3)
其中,COV = Std/Mean × 100% 为变异系数。累积分布函数为:
![]() (57.4)
(57.4)
其中,erfc为余误差函数。
一个对数正态分布的不排水抗剪强度的案例如图57.2所示,其平均值为80 kPa,变异系数为30%。
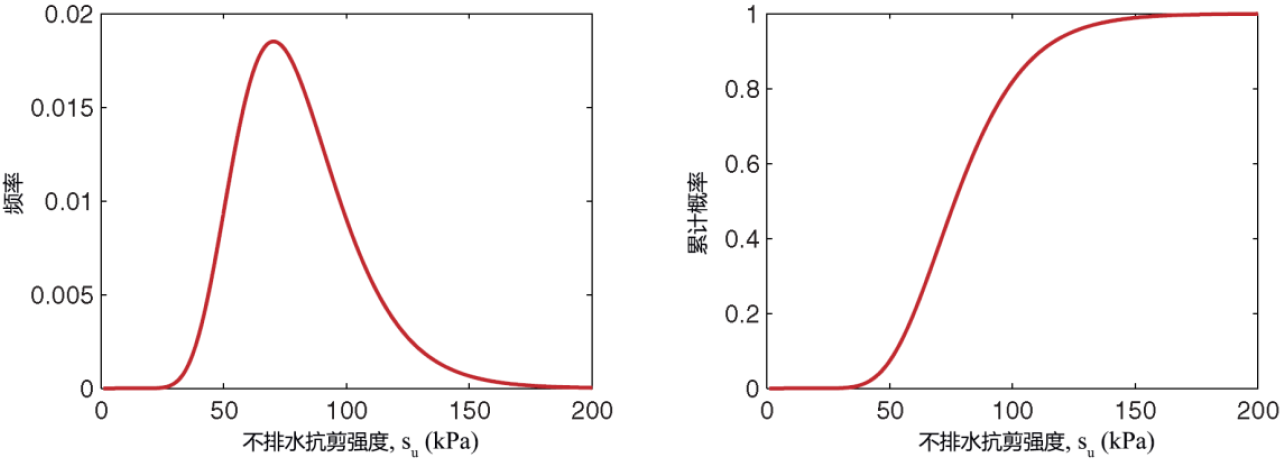
图57.2 不排水抗剪强度的对数正态分布
接下来,确定图57.1所示的问题的安全系数时,需考虑到这种可变异性,通过给定的 su 概率分布进行一系列的蒙特卡洛模拟。由于安全系数与 su 成正比,安全系数的概率分布与 su 分布相同,即参数 μ = 1.65、σ = μ × COV/100% = 0.495 的对数正态分布。如图57.3所示,一共进行了1000次的蒙特卡洛模拟,有限元计算时采用的上下限单元数量为1000,自适应迭代次数为3。如图57.3中所示,结果基于的是每个模拟的上限解和下限解的平均值。

图57.3 安全系数的概率分布。红色曲线是对数正态分布曲线,对应于假定的 su 变异率,μ = 1.65、σ = 0.495
57.2 随机场
虽然上述方法在一定程度上解释了土体强度的变异性,但在整个域中假定不排水剪切强度为恒定值是不现实的,尽管每次运行都是不同的。
随机场观点提供了一种生成更现实的材料参数空间分布的方法,考虑固有变异性时仍然采用在前一节中假定的概率分布。此外,还引入了竖直和水平相关长度,其思想是:在一个点上测量的材料参数值与相邻点的测量值存在一定的关系,这种关系取决于两点之间的距离(垂直和水平方向)。相关长度描述的距离是与测量值趋于显著相关性的。因此,较大的相关长度意味着变异场较平滑,而较小的值则意味着一个更不平整的场。在光谱的两端,一个无限的相关长度对应的情况在上一节中考虑过了(在一个给定点的值是完全相关的,即与其他任意点的值是相同的);当相关长度趋于零,则意味着没有任何关联(在域中每个点的值都是一个独立的概率分布)。不排水剪切强度随机场的一些案例如图57.4所示,在所有情况下,平均值为 80 kPa,变异系数为 30%。
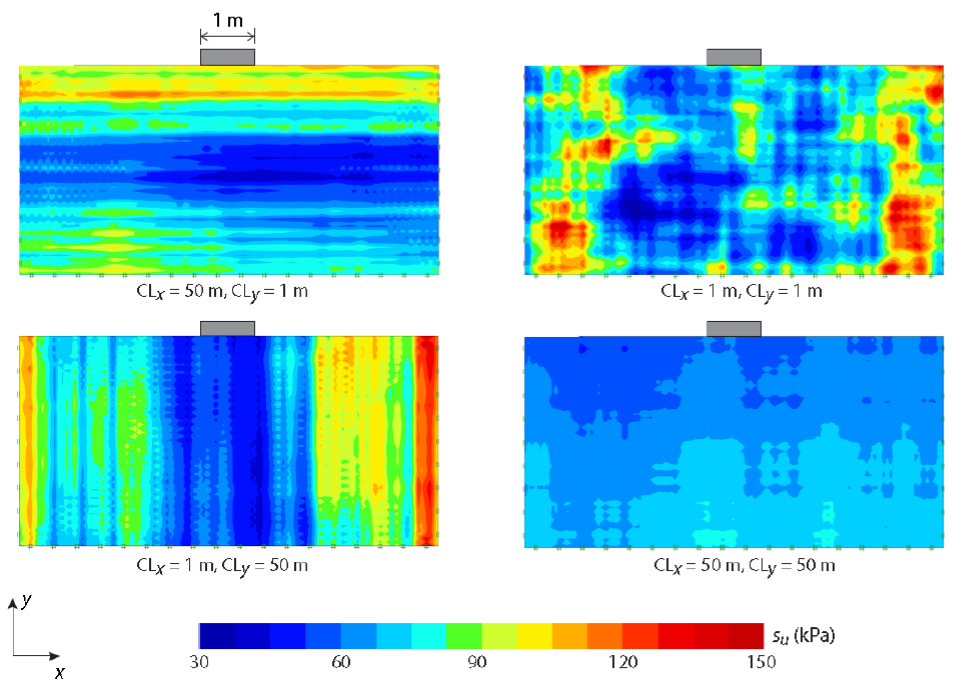
图57.4 不排水抗剪强度的随机场
生成给定材料参数的随机场,需要四个输入参数:
1. 参数的平均值
2. 参数的变异系数,COV(%)
3. 水平相关长度,CLx(m)
4. 竖直相关长度,CLy(m)
这些参数是通过区域变异对话框来定义的,如图57.1所示。
关于参数的精确值,后面三个参数是最不确定的。传统上,一般很少会去尝试量化这些参数,虽然有一些现场试验方法,特别是静力触探试验,仅仅是有一个粗略的估计。但可以肯定的是,竖直相关长度一般明显小于水平相关长度。在Phoon和Kulhawy (1999)的论文中分析了各种各样的数据,发现对于su的竖直相关长度和水平相关长度(或“波动尺度”) 分别从0.8m和46m变化到6.1m和60m。如图57.4中左上角的图,竖直和水平相关长度对应的分别是1m和50m,说明了这种相关长度对不排水抗剪强度分布的影响。关于 su 的变异系数,现有数据表明大约在10%和60%之间具有显著的分散性,并且随着 su 平均值的增加而呈现减少的趋势(如图57.5所示)。
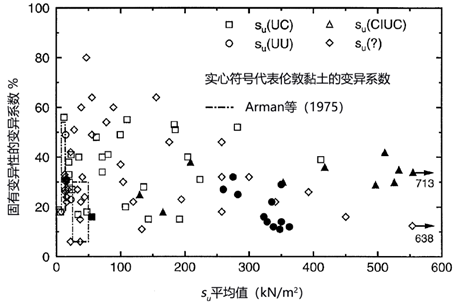
图57.5 与 su 平均值相对的 su 的变异系数(依据Phoon和Kulhawy (1999))
基于Phoon和Kulhawy (1999)提供的参考,关于su的参数如下:
平均值su = 80kPa
变异系数,COV = 30%
水平相关长度,CLx = 50m
竖直相关长度,CLy = 1m
57.3 确定性分析
首先,对具有恒定su=80 kPa的模型域进行确定性分析,计算得到的安全系数为1.65,破坏模式如图57.6所示。
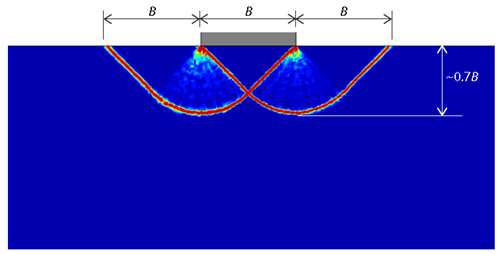
图57.6 恒定su的破坏模式
破坏模式的竖直范围约为0.7B,当测定竖直相关长度的影响时,这个值是非常有意义的。对于B ≪ CLy,FS的概率分布与 su 固有变异性的对数正态分布相同。换言之,由随机场引起的 su 变异是不会产生影响的,因为破坏比变异的尺度要浅得多。相反,对于B ≫ CLy,破坏机制覆盖了由随机场生成的所有 su 可能值,并且我们可以期望对应于某个特征平均值的FS概率分布,并且在运行过程中的变化很小,即具有较小的变异系数。
57.4 随机分析
接下来,依据上面提到的参数(平均值 su = 80kPa,COV = 30%,CLx = 50m,CLy = 1m)进行随机分析。关于合适分析类型、必要单元数量和蒙特卡洛运行次数的细节在第57.6节中会有进一步的详细讨论。
随机分析的设置可以在项目菜单下进行指定,如图57.7所示。
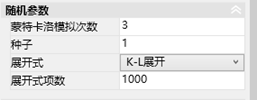
图57.7 随机分布的参数设置
种子(默认为1)是用于生成随机场的,每运行一次蒙特卡洛,数量递增1个。因此,如果要更详细地研究第n次运行,则可以将运行次数设置为1,种子一直到n。下面会采用这种方式。
各种不同基础宽度的概率分布函数的分析结果如图57.8所示,可以发现以下一些趋势:
对于宽度较小的基础,安全系数的概率分布接近于对数正态分布,相关长度无穷;
随着基础宽度的增加,安全系数的COV值逐渐减小;
平均安全系数随着基础宽度的增加而增加,而破坏的概率逐渐减小。
前两个趋势是符合预期的,但最后一个有点依赖于具体问题。事实上,一般不能保证平均安全系数随着基础宽度的增加而减小(或者对于特征系统长度和相关长度之间的比率增加)。
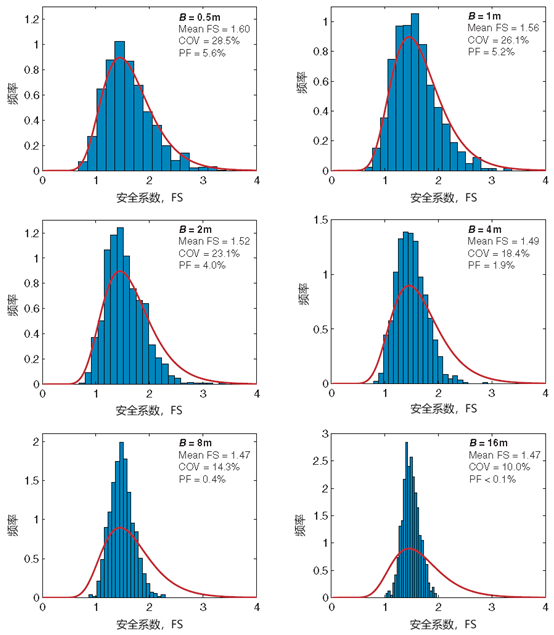
图57.8 安全系数的概率分布。红色曲线对应于无限的相关长度(或无穷小的基础宽度);在每个图中显示的是平均安全系数、COV和基于1000次运行的破坏概率(PF)。
57.5 破坏机理
由随机场模拟的 su 分布的变异性引起了各种各样的破坏机理,可以通过绘制被动区的概率分布函数(可采用XY绘图实现)来度量这个变异性,比如B=2m,如图57.9所示。
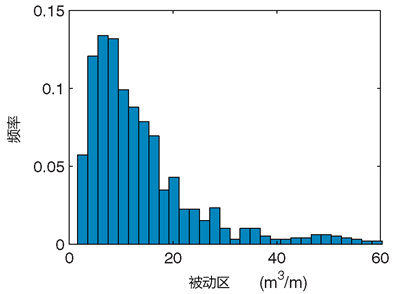
图57.9 B=2m时被动区的概率分布(不包含基础)
若要重新运行特定的蒙特卡洛实例,应将种子设置为运行次数,蒙特卡洛运行次数应设置为1(参见上一节)。图57.10中显示了三个实例,分别代表的是:
(a)由于浅层的软弱层覆盖在一个强度大的地层上,所以被动区范围很小;
(b)被动区的范围是适中的,由于覆盖于坚硬土层上的是中等强度和深度的土层;
(c)由于强层覆盖于薄弱层智商,所以被动区的范围很大。
从图57.9中我们可以看出,相比于(a)和(c)的浅层或深层机理,类似于情况(b)的破坏机理更为常见。此外,这三种机理都涉及由强度的不均匀性而引起一定量的旋转,这种特性更为符合规则。
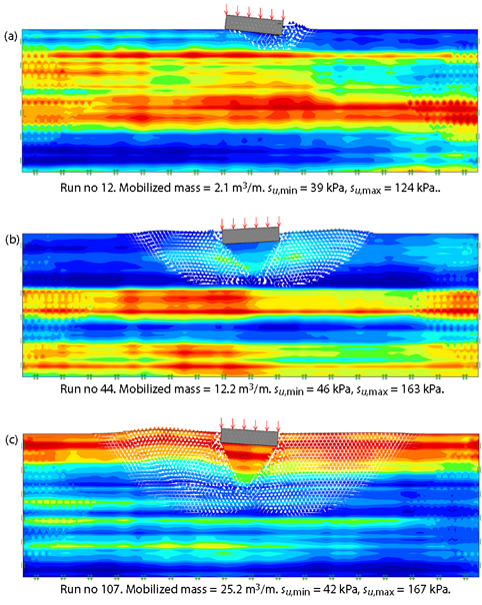
图57.10 选定B=2m的 su 分布的破坏机理(被动区范围不包括基础);着色表示在 su,min(蓝色)和su,max(红色)之间的不排水剪切强度
57.6 分析类型
对于目前的问题,安全系数与不排水抗剪强度 su 成正比,即承载力,因此,安全系数可以直接通过强度折减分析确定,或者可以通过极限分析(乘数为荷载)确定。一般来说,极限分析比强度折减更快一些,因此对于目前的随机分析是最优选的。
57.7 单元数量
对于任何确定性分析,能够提供足够精确解决方案所需要的单元数量很难提前确定。然而,作为经验法则,极限分析采用1000个单元数量和3个自适应迭代次数计算出的上下限解的平均值通常提供了精确解的更好的预估。
计算平均值为:
M = 1/2(L + U) (57.5)
其中,L和U分别是下限解和上限解,相对误差可由下式计算:
![]() (57.6)
(57.6)
这样就保证了精确解在给定的范围内:
E = M(1 ±ε) (57.7)
这里应该指出的是 ε 是最大误差,如果上限解和下限解都都包含类似大小的误差(通常情况下),则平均值将比误差 ε 所得到的值更接近精确解。
对于B=2,采用1000个单元和3次自适应迭代进行1000次的蒙特卡洛计算,最坏情况误差范围在3%到5%之间。然而,使用10000个单元,在将上限解和下限解的平均值与上下限解进行比较时,发现实际误差明显更小,这可以在图57.11中运行前20个蒙特卡洛中可以看出,使用10000个单元得到的上下限解之间的最坏情况误差大约为1%。在这些界限之间进行1000次的运行得到的平均值,实际误差最有可能小于1%。
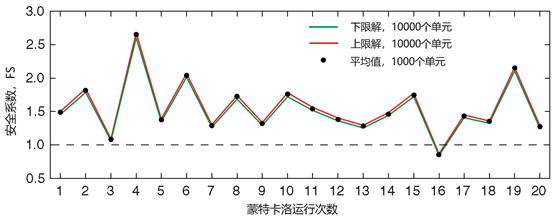
图57.11 前20次蒙特卡洛运行的安全系数,单元数量分别为1000和10000(B=2m)
57.8 运行次数
与单元数量一样,蒙特卡洛运行次数有利于提取具有合理可信度的关键统计数据(平均值、COV等),但在一定程度上也依赖于问题本身。
对于B=2 m的情况,图57.12中显示了安全系数的平均值和COV随运行次数的变化曲线。在这两种情况下,我们都可以看到,想达到可接受的准确度至少需要100-200次运行(而不是本例中所有问题的1000次运行)。另一方面,破坏概率相比相同的精度需要更多的运行次数。
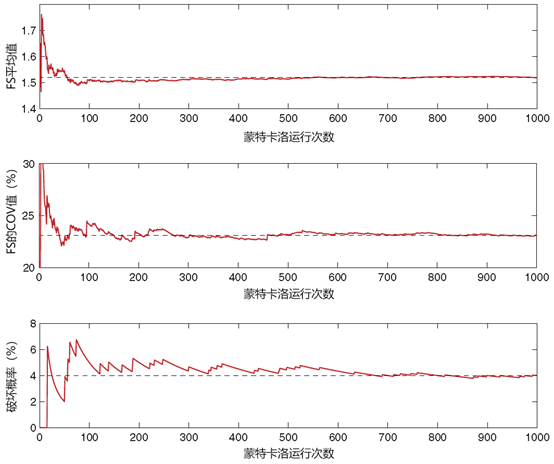
图57.12 关键统计数据随蒙特卡洛运行次数的曲线(B=2m)